Синтез цифровых схем
Такое серьезное институтское название… Не пугайтесь раньше времени. Давайте по порядку.
В электронике довольно часто используют понятие «черный ящик». Это, конечно же, не тот черный ящик, который ищут МЧСовцы после очередного крушения ТУ-154 компании «Аэрофлот». Другой ящик...
В электронике «черный ящик» – это некая схема, рисовать которую лениво. Эта схема имеет сколько-то входов, сколько-то выходов и мы точно знаем, как она себя ведет. То есть, можно легко предсказать, что получится на выходе, если чего-то подать на вход. Грубо говоря, схема черного ящика описывается математическим выражением вида:
y = f(x),
где
х – входной сигнал
y – выходной сигнал.
У черных ящиков просто уйма жизненных примеров… Взять хотя бы такую тривиальную вещь как утюг. У него есть ручечка регулировки температуры и кнопочка выброса пара – это «входы» черного ящика. Также, у него есть нагревающаяся поверхность, а в ней – дырочки – это «выходы».
Как связаны между собой входы и выходы?
Может этот пример довольно примитивен, но зато нагляден до неприличия. Ведь утром, гладя брюки, вы не задумываетесь над тем, как устроен утюг? Зато вы прекрасно знаете, что нужно сделать с ручечкой и кнопочкой, чтоб получить желаемый результат…
К чему я это все? А к тому, что в технике приходится очень часто прибегать к понятию «черного ящика» чтобы упростить разработку на определенном этапе. Однако, на последующих этапах, все равно придется «разворачивать» черный ящик – то есть, проектировать его схему.
А поскольку мы с вами носим гордое имя Электронщики, причем – не просто пайщики-лудильщики, а еще и конструктора-разработчики – то наша прямая обязанность уметь по описанию черного ящика придумать его схему.
Конечно же, утюги делать мы не будем. Тем более – в разделе по цифровой технике. Мы лучше займемся синтезом цифровых схем по таблице истинности.
Задание номер раз
Есть некий элемент с двумя входами и одним выходом, и известна его таблица истинности:
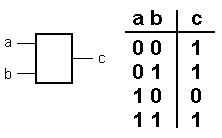
Необходимо придумать схему этого элемента на основе известных логических элементов.
Внимательно смотрим и думаем…
Нас интересуют те позиции таблицы истинности, в которых выходной сигнал равен 1.
А! Вот чего мы видим: единица на входе b в любом случае приводит к единице на выходе. Здорово!
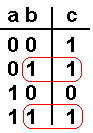
Значит, мы можем соединить вход b напрямую с выходом c … Точнее – могли бы. Но у нас есть еще одна единица на выходе – когда на оба входа поданы нули. Вспоминаем, какой элемент реагирует на два нуля? Разрешаю подглядеть в предыдущий параграф…
Правильно, элемент «ИЛИ-НЕ»! Значит, вторая единица будет формироваться элементом ИЛИ-НЕ. Давайте нарисуем для каждого случая свою схему:
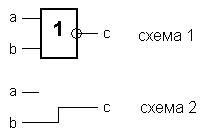
Теперь надо объединить эти схемы в одну. Помним, что непосредственно соединять цифровые выходы нельзя. Значит надо их соединить через какой-то элемент. Причем, этот элемент должен выдавать единицу на выход в случае, если хотя бы на одном входе есть единица. Ну, какой это элемент?
Конечно, это «ИЛИ».
Итак:
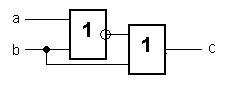
Вот и вся схема. Довольно просто, не так ли?
Дальше – хуже.
Задание номер следующее
Элемент, к которому нужно нарисовать схему, имеет три входа и один выход.
Соответственно, таблица истинности увеличивается автоматом до 8 строчек:
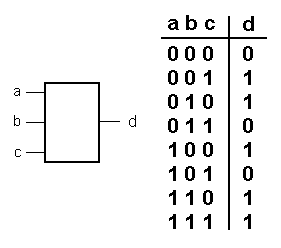
Ну как вам???
М-да, тут немного сложнее. Но! Для нас ведь нет ничего сложного, правда? Тогда – вперед и с песнями!
Итак, выделяем те строчки, в которых выходной сигнал = 1. Их всего пять:
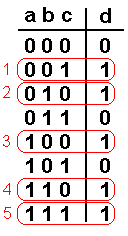
Теперь нарисуем для каждой выделенной строчки отдельную схему, используя только элементы «И» и «НЕ».
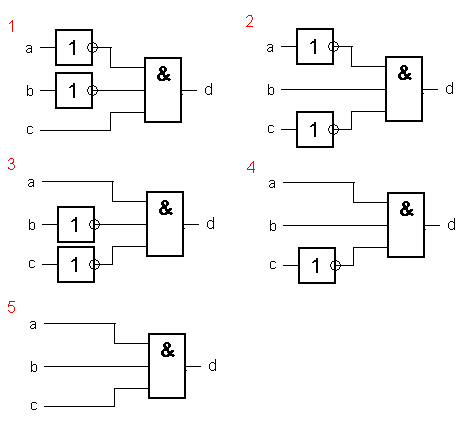
Все! Теперь только осталось объединить эти схемы в одну. При этом сразу сократится число инверторов:
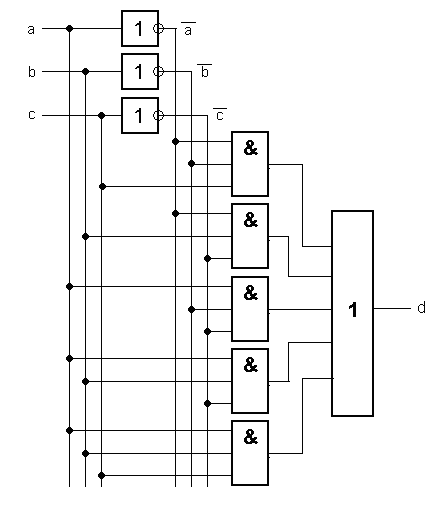
Ну как, нормально?
Объясняю: мы сделали две группы входов – прямую и инверсную (то есть «обратную»), и подключили элементы «И» к этим группам согласно схемам, которые мы разработали до этого.
Выходные сигналы элементов «И» смешиваются при помощи 5-входового элемента «ИЛИ».
Каскадирование элементов «И» и «ИЛИ»
Как вы могли заметить, в последней схеме мы использовали элементы «И» с тремя входами и элемент «ИЛИ» аж с пятью входами! У кого-то наверно возникнет вопрос: каковы их таблицы истинности?
Все в порядке, господа! Элемент «И» остается элементом «И», даже имея 100 входов. На его выходе единица возможна лишь в том случае, если на все входы поданы единицы.
То же и с элементом ИЛИ. Он выдаст единицу в случае, если хотя бы на одном входе будет единица, будь у него хоть тыща входов.
Такие многовходовые элементы можно легко получить из обычных двухвходовых, включив их в каскадную схему:
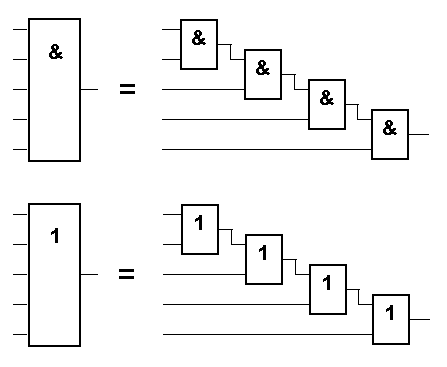
Если вы не верите – составьте таблицу истинности для каждой «ступеньки» каскада – и проверьте :)
Источник: www.radiokot.ru