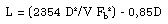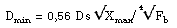| Портал для радиолюбителей |
От редакции: Статья итальянского специалиста-акустика, воспроизводимая здесь с благословения автора, в оригинале называлась Teoria e pratica del condotto di accordo. То есть, в буквальном переводе – «Теория и практика фазоинвертора». Заголовок этот, на наш взгляд, соответствовал содержанию статьи только формально. Действительно, речь идет о соотношении простейшей теоретической модели фазоинвертора и тех сюрпризов, которые готовит практика. Но это – если формально и поверхностно. А по существу, статья содержит ответ на вопросы, которые возникают, судя по редакционной почте, сплошь и рядом при расчете и изготовлении сабвуфера-фазоинвертора. Вопрос первый: «Если рассчитать фазоинвертор по формуле, известной уже давным-давно, получится ли у готового фазоинвертора расчетная частота?» Наш итальянский коллега, съевший на своем веку собак эдак с десяток на фазоинверторах, отвечает: «Нет, не получится». А потом объясняет, почему и, что самое ценное, на сколько именно не получится. Вопрос второй: «Рассчитал тоннель, а он такой длинный, что никуда не помещается. Как быть?» И здесь синьор предлагает настолько оригинальные решения, что именно эту сторону его трудов мы и вынесли в заголовок. Так что ключевое слово в новом заголовке надо понимать не по-новорусски (иначе мы бы написали: «короче – фазоинвертор»), а совершенно буквально. Геометрически. А теперь слово для выступления имеет синьор Матараццо.
Фазоинвертор: короче!
|
Жан-Пьеро МАТАРАЦЦО Перевод с итальянского Е. Журковой |
|
Об авторе: Жан-Пьеро Матараццо родился в 1953 г. в городе Авеллино, Италия. С начала 70-х работает в области профессиональной акустики. Долгие годы был ответственным за тестирование акустических систем для журнала «Suono» («Звук»). В 90-х годах разработал ряд новых математических моделей процесса излучения звука диффузорами громкоговорителей и несколько проектов акустических систем для промышленности, включая популярную в Италии модель «Опера». С конца 90-х активно сотрудничает с журналами «Audio Review», «Digital Video» и, что для нас наиболее важно, «ACS» («Audio Car Stereo»). Во всех трех он – главный по измерению параметров и тестированию акустики. Что еще?.. Женат. Два сынишки растут, 7 годиков и 10.
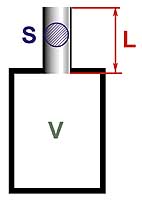
Рис 1. Схема резонатора Гельмгольца. То, от чего все происходит.
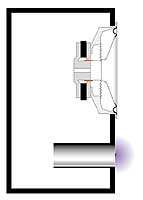
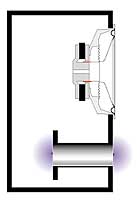
Рис 2. Классическая конструкция фазоинвертора. При этом часто не учитывают влияние стенки.
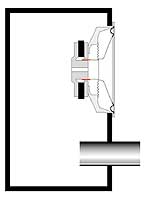
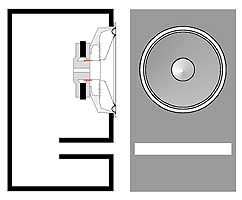
Рис 3. Фазоинвертор с тоннелем, концы которого находятся в свободном пространстве. Здесь влияния стенок нет.
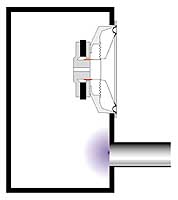
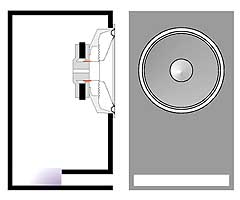
Рис 4. Можно вывести тоннель полностью наружу. Здесь опять произойдет «виртуальное удлинение».
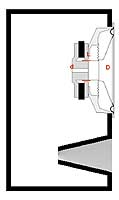
Рис 5. Можно получить «виртуальное удлинение» на обоих концах тоннеля, если сделать еще один фланец.
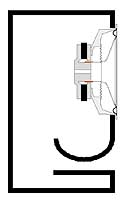
Рис 6. Щелевой тоннель, расположенный далеко от стенок ящика.
Рис 7. Щелевой тоннель, расположенный вблизи стенки. В результате влияния стенки его «акустическая» длина получается больше геометрической.
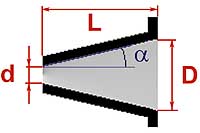
Рис 8. Тоннель в форме усеченного конуса.
Рис 9. Основные размеры конического тоннеля.
Рис 10. Размеры щелевого варианта конического тоннеля.
Рис 11. Экспоненциальный тоннель.
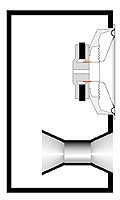
Рис 12. Тоннель в форме песочных часов.
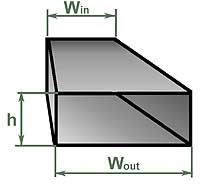
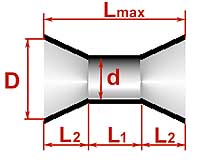
Рис 13. Основные размеры тоннеля в форме песочных часов.
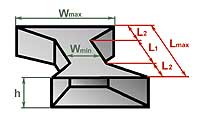
Рис 14. Щелевой вариант песочных часов. |
Магические формулы Одно из наиболее часто встречающихся пожеланий в электронной почте автора – привести «магическую формулу», по которой читатель ACS мог бы сам рассчитать фазоинвертор. Это, в принципе, нетрудно. Фазоинвертор представляет собой один из случаев реализации устройства под названием «резонатор Гельмгольца». Формула его расчета не намного сложнее самой распространенной и доступной модели такого резонатора. Пустая бутылочка из-под кока-колы (только обязательно бутылка, а не алюминиевая банка) – именно такой резонатор, настроенный на частоту 185 Гц, это проверено. Впрочем, резонатор Гельмгольца намного древнее даже этой, постепенно выходящей из употребления упаковки популярного напитка. Однако и классическая схема резонатора Гельмгольца схожа с бутылкой (рис. 1). Для того чтобы такой резонатор работал, важно, чтобы у него был объем V и тоннель с площадью поперечного сечения S и длиной L. Зная это, частоту настройки резонатора Гельмгольца (или фазоинвертора, что одно и то же) теперь можно рассчитать по формуле:
где Fb – частота настройки в Гц, с – скорость звука,
равная 344 м/с, S – площадь тоннеля в кв. м, L – длина тоннеля в м,
V – объем ящика в куб. м. Эта формула действительно магическая, в том смысле, что настройка фазоинвертора не зависит от параметров динамика, который будет в него установлен. Объем ящика и размеры тоннеля частоту настройки определяют раз и навсегда. Все, казалось бы, дело сделано. Приступаем. Пусть у нас есть ящик объемом 50 литров. Мы хотим превратить его в корпус фазоинвертора с настройкой на 50 Гц. Диаметр тоннеля решили сделать 8 см. По только что приведенной формуле частота настройки 50 Гц получится, если длина тоннеля будет равна 12,05 см. Аккуратно изготавливаем все детали, собираем их в конструкцию, как на рис. 2, и для проверки измеряем реально получившуюся резонансную частоту фазоинвертора. И видим, к своему удивлению, что она равна не 50 Гц, как полагалось бы по формуле, а 41 Гц. В чем дело и где мы ошиблись? Да нигде. Наш свежепостроенный фазоинвертор оказался бы настроен на частоту, близкую к полученной по формуле Гельмгольца, если бы он был сделан, как показано на рис. 3. Этот случай ближе всего к идеальной модели, которую описывает формула: здесь оба конца тоннеля «висят в воздухе», относительно далеко от каких-либо преград. В нашей конструкции один из концов тоннеля сопрягается со стенкой ящика. Для воздуха, колеблющегося в тоннеле, это небезразлично, из-за влияния «фланца» на конце тоннеля происходит как бы его виртуальное удлинение. Фазоинвертор окажется настроенным так, как если бы длина тоннеля была равна 18 см, а не 12, как на самом деле. Заметим, что то же самое произойдет, если тоннель полностью разместить снаружи ящика, снова совместив один его конец со стенкой (рис. 4). Существует эмпирическая зависимость «виртуального удлинения» тоннеля в зависимости от его размеров. Для круглого тоннеля, один срез которого расположен достаточно далеко от стенок ящика (или других препятствий), а другой находится в плоскости стенки, это удлинение приблизительно равно 0,85D. Теперь, если подставить в формулу Гельмгольца все константы, ввести поправку на «виртуальное удлинение», а все размеры выразить в привычных единицах, окончательная формула для длины тоннеля диаметром D, обеспечивающего настройку ящика объемом V на частоту Fb, будет выглядеть так:
Здесь частота – в герцах, объем – в литрах, а длина и диаметр тоннеля – в миллиметрах, как нам привычнее. Полученный результат ценен не только тем, что позволяет на этапе расчета получить значение длины, близкое к окончательной, дающей требуемое значение частоты настройки, но и тем, что открывает определенные резервы укорочения тоннеля. Почти один диаметр мы уже выиграли. Можно укоротить тоннель еще больше, сохранив ту же частоту настройки, если сделать фланцы на обоих концах, как показано на рис. 5. Теперь, кажется, все учтено, и, вооруженные этой формулой, мы представляемся себе всесильными. Именно здесь нас и ждут трудности. Первые трудности Первая (и главная) трудность заключается в следующем: если относительно небольшой по объему ящик требуется настроить на довольно низкую частоту, то, подставив в формулу для длины тоннеля большой диаметр, мы и длину получим большую. Попробуем подставить диаметр поменьше – и все получается отлично. Большой диаметр требует большой длины, а маленький – как раз небольшой. Что же тут плохого? А вот что. Двигаясь, диффузор динамика своей тыльной стороной «проталкивает» практически несжимаемый воздух через тоннель фазоинвертора. Поскольку объем колеблющегося воздуха постоянен, то скорость воздуха в тоннеле будет во столько раз больше колебательной скорости диффузора, во сколько раз площадь сечения тоннеля меньше площади диффузора. Если сделать тоннель в десятки раз меньшего размера, чем диффузор, скорость потока в нем окажется большой, и, когда она достигнет 25 – 27 метров в секунду, неизбежно появление завихрений и струйного шума. Великий исследователь акустических систем Р. Смолл показал, что минимальное сечение тоннеля зависит от диаметра динамика, наибольшего хода его диффузора и частоты настройки фазоинвертора. Смолл предложил совершенно эмпирическую, но безотказно работающую формулу для вычисления минимального размера тоннеля:
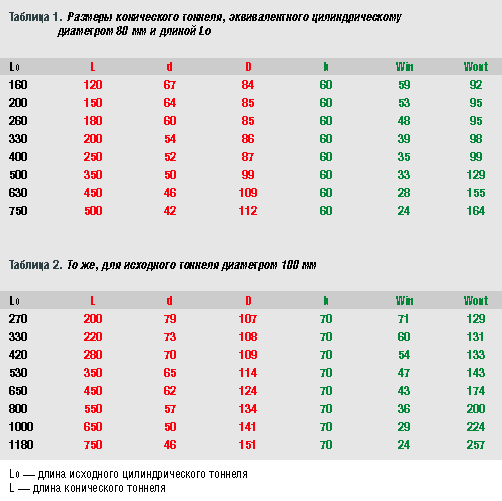
Формулу свою Смолл вывел в привычных для него единицах, так что диаметр динамика Ds, максимальный ход диффузора Xmax и минимальный диаметр тоннеля Dmin выражаются в дюймах. Частота настройки фазоинвертора – как обычно, в герцах. Теперь все выглядит не так радужно, как прежде. Очень часто оказывается, что, если правильно выбрать диаметр тоннеля, он выходит невероятно длинным. А если уменьшить диаметр, появляется шанс, что уже на средней мощности тоннель «засвистит». Помимо собственно струйных шумов, тоннели небольшого диаметра обладают еще и склонностью к так называемым «органным резонансам», частота которых намного выше частоты настройки фазоинвертора и которые возбуждаются в тоннеле турбулентностями при больших скоростях потока. Столкнувшись с такой дилеммой, читатели ACS обычно звонят в редакцию и просят подсказать им решение. У меня их три: простое, среднее и экстремальное. Простое решение для небольших проблем Когда расчетная длина тоннеля получается такой, что он почти помещается в корпусе и требуется лишь незначительно сократить его длину при той же настройке и площади сечения, я рекомендую вместо круглого использовать щелевой тоннель, причем размещать его не посреди передней стенки корпуса (как на рис. 6), а вплотную в одной из боковых стенок (как на рис. 7). Тогда на конце тоннеля, находящемся внутри ящика, будет сказываться эффект «виртуального удлинения» из-за находящейся рядом с ним стенки. Опыты показывают, что при неизменной площади сечения и частоте настройки тоннель, показанный на рис. 7, получается примерно на 15% короче, чем при конструкции, как на рис. 6. Щелевой фазоинвертор, в принципе, менее склонен к органным резонансам, чем круглый, но, чтобы обезопасить себя еще больше, я рекомендую устанавливать внутри тоннеля звукопоглощающие элементы, в виде узких полосок фетра, наклеенных на внутреннюю поверхность тоннеля в районе трети его длины. Это – простое решение. Если его недостаточно, придется перейти к среднему. Среднее решение для проблем побольше Решение промежуточной сложности заключается в использовании тоннеля в форме усеченного конуса, как на рис. 8. Мои эксперименты с такими тоннелями показали, что здесь можно уменьшить площадь сечения входного отверстия по сравнению с минимально допустимой по формуле Смолла без опасности возникновения струйных шумов. Кроме того, конический тоннель намного менее склонен к органным резонансам, нежели цилиндрический. В 1995 году я написал программу для расчета конических тоннелей. Она заменяет конический тоннель последовательностью цилиндрических и путем последовательных приближений вычисляет длину, необходимую для замены обычного тоннеля постоянного сечения. Программа эта сделана для всех желающих, и ее можно взять на сайте журнала ACS в разделе ACS Software. Маленькая программка, работает под DOS, можно скачать и посчитать самому. А можно поступить по-другому. При подготовке русской редакции этой статьи результаты вычислений по программе CONICO были сведены в таблицу, из которой можно взять готовый вариант. Таблица составлена для тоннеля диаметром 80 мм. Это значение диаметра подходит для большинства сабвуферов с диаметром диффузора 250 мм. Рассчитав по формуле требуемую длину тоннеля, найдите это значение в первом столбце. Например, по вашим расчетам оказалось, что нужен тоннель длиной 400 мм, например, для настройки ящика объемом 30 литров на частоту 33 Гц. Проект нетривиальный, и разместить такой тоннель внутри такого ящика будет непросто. Теперь смотрим в следующие три столбца. Там приведены рассчитанные программой размеры эквивалентного конического тоннеля, длина которого будет уже не 400, а всего 250 мм. Совсем другое дело. Что означают размеры в таблице, показано на рис. 9.
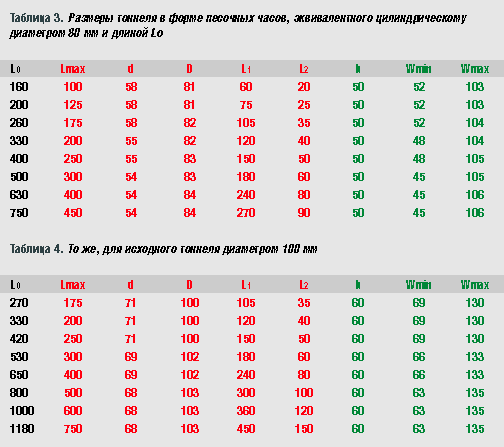
Таблица 2 составлена для исходного тоннеля диаметром 100 мм. Это подойдет для большинства сабвуферов с головкой диаметром 300 мм. Если решите пользоваться программой самостоятельно, помните: тоннель в форме усеченного конуса делается с углом наклона образующей a от 2 до 4 градусов. Этот угол больше 6 – 8 градусов делать не рекомендуется, в этом случае возможно возникновение завихрений и струйных шумов на входном (узком) конце тоннеля. Однако и при небольшой конусности уменьшение длины тоннеля получается довольно значительным. Тоннель в форме усеченного конуса не обязательно должен иметь круглое сечение. Как и обычный, цилиндрический, его иногда удобнее делать в виде щелевого. Даже, как правило, удобнее, ведь тогда он собирается из плоских деталей. Размеры щелевого варианта конического тоннеля приведены в следующих столбцах таблицы, а что эти размеры означают, показано на рис. 10. Замена обычного тоннеля коническим способна решить много проблем. Но не все. Иногда длина тоннеля получается настолько большой, что укорочения его даже на 30 – 35% недостаточно. Для таких тяжелых случаев есть... ...экстремальное решение для больших проблем Экстремальное решение заключается в применении тоннеля с экспоненциальными обводами, как показано на рис. 11. У такого тоннеля площадь сечения сначала плавно уменьшается, а потом так же плавно возрастает до максимальной. С точки зрения компактности для данной частоты настройки, устойчивости к струйным шумам и органным резонансам экспоненциальный тоннель не имеет себе равных. Но он не имеет себе равных и по сложности изготовления, даже если рассчитать его обводы по такому же принципу, как это было сделано в случае конического тоннеля. Для того чтобы преимуществами экспоненциального тоннеля все же можно было воспользоваться на практике, я придумал его модификацию: тоннель, который я назвал «песочные часы» (рис. 12). Тоннель-песочные часы состоит из цилиндрической секции и двух конических, откуда внешнее сходство с древним прибором для измерения времени. Такая геометрия позволяет укоротить тоннель по сравнению с исходным, постоянного сечения, по меньшей мере, в полтора раза, а то и больше. Для расчета песочных часов я тоже написал программу, ее можно найти там же, на сайте ACS. И так же, как для конического тоннеля, здесь приводится таблица с готовыми вариантами расчета.
Что означают размеры в таблицах 3 и 4, станет ясно из рис. 13. D и d – это диаметр цилиндрической секции и наибольший диаметр конической секции, соответственно, L1 и L2 – длины секций. Lmax – полная длина тоннеля в форме песочных часов, приводится просто для сравнения, насколько короче его удалось сделать, а вообще, это L1 + 2L2. Технологически песочные часы круглого поперечного сечения делать не всегда просто и удобно. Поэтому и здесь можно выполнить его в виде профилированной щели, получится, как на рис. 14. Для замены тоннеля диаметром 80 мм я рекомендую высоту щели выбрать равной 50 мм, а для замены 100-миллиметрового цилиндрического тоннеля – равной 60 мм. Тогда ширина секции постоянного сечения Wmin и максимальная ширина на входе и выходе тоннеля Wmax будут такими, как в таблице (длины секций L1 и L2 – как в случае с круглым сечением, здесь ничего не меняется). Если понадобится, высоту щелевого тоннеля h можно изменить, одновременно скорректировав и Wmin, Wmax так, чтобы значения площади поперечного сечения (h.Wmin, h.Wmax) остались неизменными. Вариант фазоинвертора с тоннелем в форме песочных часов я применил, например, когда делал сабвуфер для домашнего театра с частотой настройки 17 Гц. Расчетная длина тоннеля получилась больше метра, а рассчитав «песочные часы», я смог сократить ее почти вдвое, при этом шумов не было даже при мощности около 100 Вт. Надеюсь, вам это тоже поможет... |
Добавил: Павел (Admin)

Автор: Жан-Пьеро МАТАРАЦЦО Перевод с итальянского Е. Журковой
Вас может заинтересовать:
- Ремонт и перемотка звуковой катушки громкоговорителя
- Второе дыхание 75АС-001
- Механическое демпфирование диффузоров
- Фронтальная акустика: подиумы
- О басе в подробностях
| © PavKo, 2007-2018 Обратная связь Ссылки |
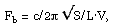
 = 3,14,
это само собой.
= 3,14,
это само собой.