| Портал для радиолюбителей |
Начнем опять с десятеричной системы.
Возьмем для примера то же число 167 (не знаю, почему именно оно пришло мне в голову), и представим это число так:
167 = 1*100 + 6*10 + 7*1
Не правда ли, это справедливо? Ну значит, справедливо и следующее:
167 = 1*102 + 6*101 + 7*100
(любое число в 0-й степени равно 1).
Что мы сделели? Мы умножили значение каждого разряда на основание системы счисления, возведенное в степень, равную номеру разряда (если младший разряд принять за 0-й). Не понятно?…
Объясняю.
Число 167 имеет три разряда. Нумерация разрядов всегда идет справа-налево, от младшего к старшему. Все нормальные люди считают с единицы. Ненормальные, то есть – мы, электронщики-программисты, считают с нуля. Запомните это. С НУЛЯ!!! Все и всегда! Так вот, именно поэтому младший разряд будет – нулевой.
Итого получаем:
0 разряд = 7
1 разряд = 6
2 разряд = 1
Система счисления – десятичная. Значит, ее основание – 10. Возводим 10 в степень, равную номеру каждого разряда и умножаем на то, что получилось значение разряда. Потом все это складываем. Вот так просто!
Переходим (возвращаемся) к двоичной системе.
Все абсолютно так же.
Число 10100 можно представить как:
1*24 + 0*23 + 1*22 + 0*21 + 0*20
или
16 + 0 + 4 + 0 + 0.
Путем чрезвычайно сложных расчетов, можно получить сумму этого всего. Она равна 20.
Итак, господа. Только что мы преобразовали двоичное число в десятеричное.
Оказалось, что 101002 = 2010.
Сделать это проще простого, если знать степени двойки. Лично я наизусть с ходу называю все целые степени двойки от 0 до 18. Дальше мне не особо нужно, а если нужно – всегда можно вычислить. А пока что, запомните хотя бы до 16-й:
20 = 1
21 = 2
22 = 4
23 = 8
24 = 16
25 = 32
26 = 64
27 = 128
28 = 256
29 = 512
210 = 1024
211 = 2048
212 = 4096
213 = 8192
214 = 16384
215 = 32768
216 = 65536
и т.д.
Ну теперь давайте преобразуем 8-разрядное двоичное число в десятеричное. Для этого нарисуем такую табличку:
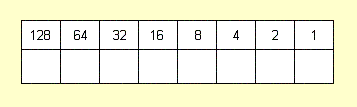
В верхней строчке таблицы – множители, на которые нужно помножать значения разрядов.
Возьмем, к примеру, число 10100111.
Вписываем его в таблицу:
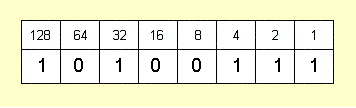
Теперь умножаем значение разряда на множитель этого разряда и складываем результаты:
1*128 + 0*64 + 1*32 + 0*16 + 0*8 + 1*4 + 1*2 + 1*1 =
= 128 + 32 + 4 + 2 + 1 = 167.
Опа! Получилось наше родимое число 167. Чудеса! :)
Все! Преоборазовали!
Посмотрите, что мы в результате сделали. В результате – мы просто сложили множители тех разрядов, в которых стояли едиицы. Такой метод преобразования – самый легкий и простой. И если на уроках информатики вас долго и безрезультатно учили делать кучу операций в столбик – забудьте. Все гораздо проще!
Преобразование 10 ->2
Теперь проделаем то же самое, но – в обратную сторону. Возьмем мы то же самое число 167, и внимательно на него посмотрим. Посмотрели? Теперь посмотрите в таблицу (а лучше - вспомните), какая наибольшая степень двойки еще меньше этого числа.
Очевидно, это 128. Значит, опять рисуем таблицу.
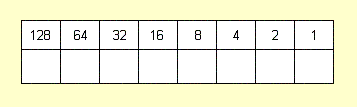
Множитель старшего разряда в ней будет равен 128. Далее – 64, 32, и т.д… Всего – 8 разрядов.
Сразу ставим в старший разряд 1. Дальше станет понятно почему.
Теперь отнимаем от 167 множитель 128.
167 - 128 = 39
Так как 39 меньше следующего множителя (64), в следующий разряд пишем 0.
Так как ничего не отняли – остаток прежний – 39. Смотрим следующий множитель: 32. Он меньше, чем 39, значит его можно отнять. Отнимаем, и ставим в разряд единицу:
Осталось число 7. Оно явно меньше чем 16 или 8, поэтому два следующих разряда будут равны 0:
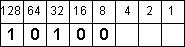
Дальше:
7 - 4 = 3
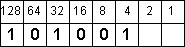
3 - 2 = 1
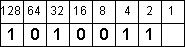
1 - 1 = 0
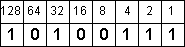
Заметим. В конечном итоге у нас должен получиться НОЛЬ! Если ноль не получился – значит мы где-то напортачили.
Вот. Не смею вас более мучить. Пока что – это все.
Источник: www.radiokot.ru
Добавил: Павел (Admin)
Автор:
Вас может заинтересовать:
- Начинающим программистам микроконтроллеров PIC
- Расширители импульсов
- Устранение дребезга контактов
- Формирователи длинных импульсов (одновибраторы)
- Формирователи пачки импульсов
| © PavKo, 2007-2018 Обратная связь Ссылки |